Dynamic Beta Estimation in Financial Markets using Kalman Filter Regression

In this project, I implemented a dynamic linear regression model using the Kalman Filter to estimate the time-varying relationship between financial assets and market indices. The objective was to track how the sensitivity (beta) of a stock—such as Google (GOOGL)—evolves in response to broader market movements like the S&P 500 (^GSPC). Starting with a curated dataset of multiple assets and indices, I performed extensive data cleaning to handle NaNs, missing values, and mismatched trading calendars using techniques like forward/backward fill and interpolation. After establishing a baseline with standard linear regression, I applied a custom Kalman Filter to the time series, allowing the beta coefficient to adapt over time to new data. This dynamic approach better reflects real market behavior, especially in volatile or non-stationary periods. The notebook also includes detailed visualizations such as asset price series, regression diagnostics, and a plot showing the evolving beta in real-time. Through this project, I demonstrated the application of Bayesian filtering techniques in financial modeling, combined with strong skills in time-series analysis, regression modeling, and Python-based data science using libraries like statsmodels, scipy, and custom Kalman modules.

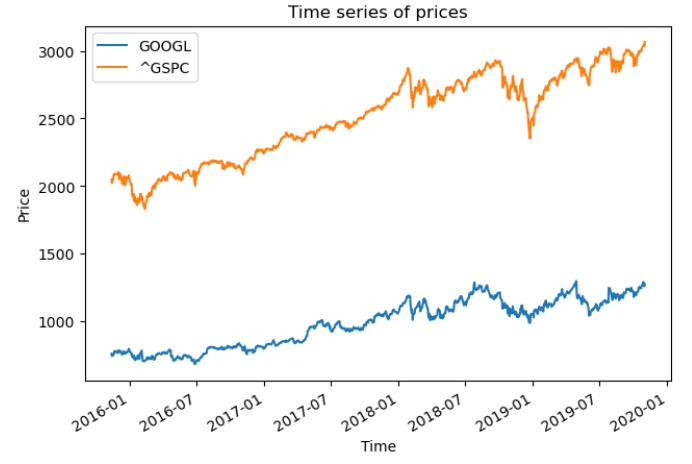
This project showcases how asset-market relationships evolve over time, outperforming static linear regression.