Classical Mean-Variance Portfolio Optimization using Python
In this project, I implemented and analyzed the Classical Mean-Variance Optimization (MVO) model based on Modern Portfolio Theory (MPT) using Python. The goal was to determine the optimal portfolio weights that maximize expected return for a given level of risk. Using real daily stock price data, I calculated log-returns, normalized prices, and conducted correlation analysis to understand asset relationships. The project included a detailed mathematical foundation covering log vs. linear returns, portfolio weighting, and conversion of daily return statistics to a monthly investment horizon. Optimization was performed using both scipy.optimize and cvxpy libraries to maximize the Sharpe ratio and generate the tangency portfolio under different constraints, including no-short-selling. To assess model assumptions, I conducted normality tests using the Shapiro-Wilk method and visualized the probability distribution of portfolio returns. Key diagrams included normalized price trends across stocks, correlation heatmaps, and portfolio return distributions, all of which provided critical insights into portfolio construction. This work showcases my ability to integrate financial theory with quantitative modeling, apply advanced optimization techniques, and create visually-driven investment strategies using Python and modern data science tools.
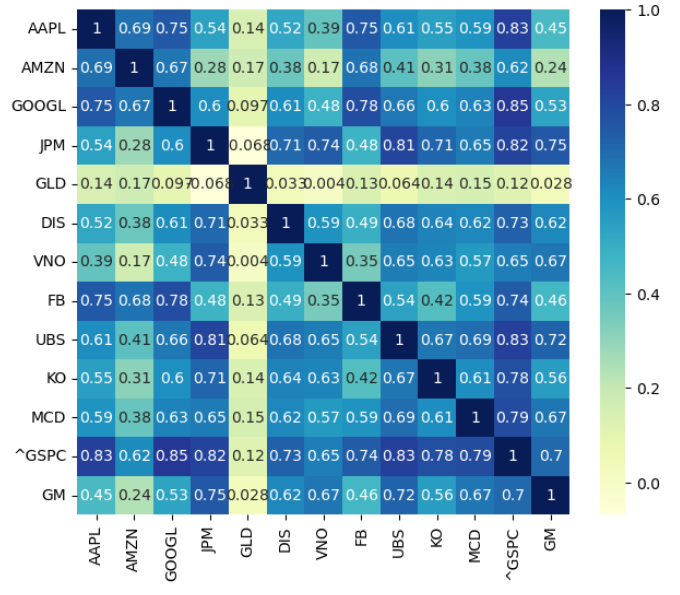
This heatmap visualizes the correlation matrix of returns among various assets, including stocks, indices, and commodities.

